あしたに日記

■ 食玩問題

skimsrの日記より。
ある食玩にはM種類のバリエーションがあり，それぞれは等頻度で
出現するとする。つまり，食玩を1つ購入すると，どの種類も1/M
の確率で出現するとする。このとき，食玩をN個購入したときに初
めて全種類が揃う(コンプリートする)確率 P(M,N) を求めよ。
算数はあんまし得意ではないのですが、やってみよう。

＝＝＝＝(注：下記内容は間違っていることがすてに指摘されています!!)＝＝＝＝

ザク、グフ、ドムの三種類しかない食玩があったとして、5箱買ったとする。

• : 5箱の中にザクが一つでも入っている確率
• : 5箱の中にグフが一つでも入っている確率
• : 5箱の中にドムが一つでも入っている確率 とすると、コンプリートした確率は、これらを全てかけたもの、すなわち である。（すべての食玩の出る確率は平等だから）

ここで、えーと、高校あたりの算数を思い出すと、

なので、コンプリートした確率は、以下のようになる。

一般的に書くと、

かな。

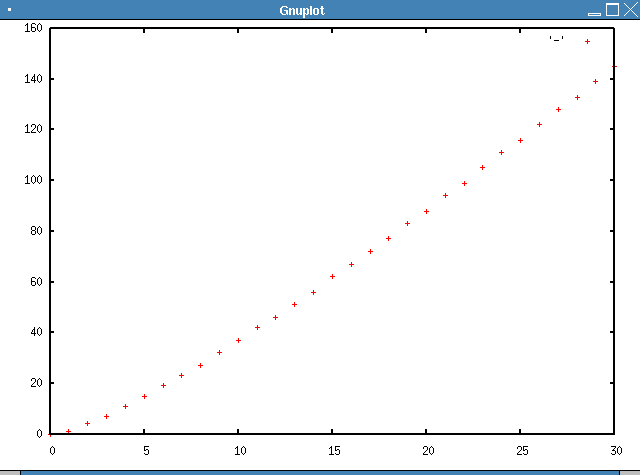
む。こちらと解析解のカタチが違う。同じ条件でプロットすると、こういう感じになる。だいたい同じようですが。算数はよくわからないので合ってることにしよう。

さて、ものすごーく話を単純に、x種類の食玩をコンプリートするには何個買えばいいの？っていうことを考えてみる。
「コンプリートする確率が85％以上」であれば良し、とすると、
下のようなグラフになる。なるほど、ざっくり４倍ぐらいの数を買うことになるわけね。だいたい線形なのが興味深いところ。